スプライン曲線はいくつかの式を組み合わせて自由な曲線をなるべく簡単に作ろうとする手法です。画像でいえば赤の曲線と青の曲線とまた別の赤の曲線を組み合わせて複雑な曲線を作っています。
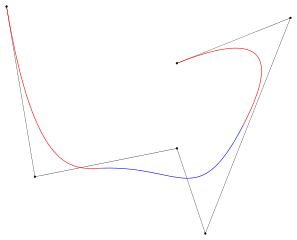
B-スプライン曲線 – Wikipedia
ざっくばらんに中身の式の例を書けば次の様になります。適当に分けられた区分の中でそれぞれ別の式が定義されているわけです。
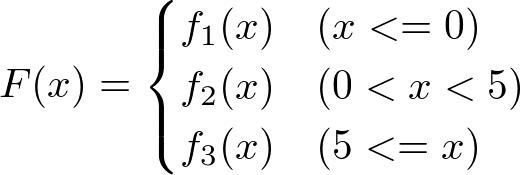
このそれぞれの式の作り方を与えられた点群に近似し、連続した値にする、という目的を達成する作り方としてPython上で扱います。
コード例は次です。
scipy.interpolate.UnivariateSpline — SciPy v1.4.1 Reference Guide
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
import numpy as np
def main():
# テストデータの適当な点を作成
x = np.linspace(-3, 3, 50)
y = np.exp(-x ** 2) + 0.1 * np.random.randn(50)
# 点をプロット
plt.plot(x, y, 'ro', ms=5)
# スプライン曲線を定義. ライブラリからの呼び出しだけでOK.
# kは滑らかさを定義する引数
spl = UnivariateSpline(x, y, k=5)
# スプライン曲線を描画するX軸の値を定義
xs = np.linspace(-3, 3, 1000)
# スプライン曲線をプロット
plt.plot(xs, spl(xs), 'g', lw=3)
# プロットした諸々を表示
plt.show()
if __name__ == '__main__':
main()
結果は次の画像です。ランダムノイズ等がのった荒れた点を滑らかに表現するのに便利です(単に表現するだけでなく滑らかにする方法を探索する場合はさすがに別の畑ですが)。無理に移動平均を取るなどして重い処理をする必要もありません。
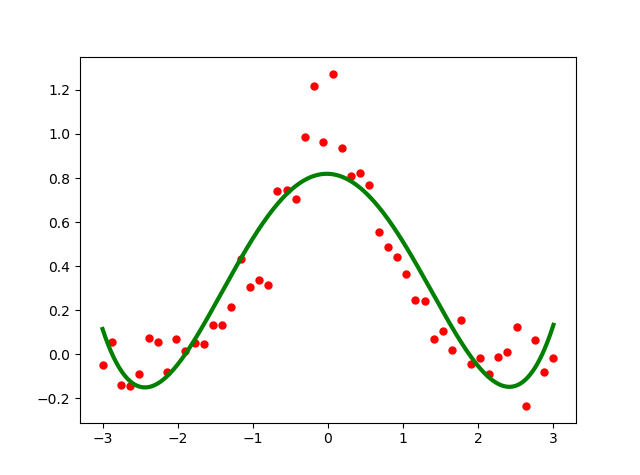
少々複雑になりますが例で使用した UnivariateSpline 関数以外にも制御と表現が複雑になった他関数がいくつもあります。
Interpolation (scipy.interpolate) — SciPy v1.4.1 Reference Guide




